本文为知乎版本的纠错和 markdown 版本 在学习深度学习相关知识，无疑都是从神经网络开始入手，在神经网络对参数的学习算法bp算法，接触了很多次，每一次查找资料学习，都有着似懂非懂的感觉，这次趁着思路比较清楚，也为了能够让一些像我一样疲于各种查找资料，却依然懵懵懂懂的孩子们理解，参考了梁斌老师的博客BP算法浅谈（Error Back-propagation）（为了验证梁老师的结果和自己是否正确，自己python实现的初始数据和梁老师定义为一样！），进行了梳理和python代码实现，一步一步的帮助大家理解bp算法！

为了方便起见，这里我定义了三层网络，输入层（第0层），隐藏层（第1层），输出层（第二层）。并且每个结点没有偏置（有偏置原理完全一样），激活函数为sigmod函数（不同的激活函数，求导不同），符号说明如下：

$W_{ab}$	代表的是结点 a 点结点 b 的权重
$y_a$	代表结点 a 的输出值
$z_a$	代表结点 a 的输入值
$\delta_a$	代表结点 a 的错误(反向传播用到)
C	最终损失函数
$f(x) = \frac{1}{1+e^{-x}}$	结点的激活函数
$W2$	左边字母, 右边数字, 代表第几层的矩阵或者向量

对应的网络如下:

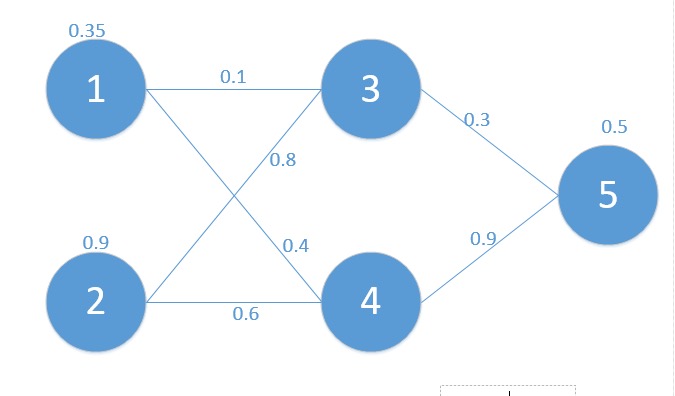
其中对应的矩阵表示如下：

$$X = Z_0 = \begin{bmatrix} 0.35 \\ 0.9 \end{bmatrix}$$

$$y_{out} = 0.5$$

$$W0 = \begin{bmatrix} w_{31} & w_{32} \\ w_{41} & w_{42} \end{bmatrix} = \begin{bmatrix} 0.1 & 0.8 \\ 0.4 & 0.6 \end{bmatrix}$$

$$W1 = \begin{bmatrix} w_{53} & w_{54} \end{bmatrix} = \begin{bmatrix} 0.3 & 0.9 \end{bmatrix}$$

首先我们先走一遍正向传播, 公式与相应的数据对应如下：

$$\begin{align*} z1 &= \begin{bmatrix} z_3 \\ z_4 \end{bmatrix} = W0 \times X = \begin{bmatrix} w_{31} & w_{32} \\ w_{41} & w_{42} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\ &= \begin{bmatrix} w_{31} \times x_1 + w_{32} \times x_2 \\ w_{41} \times x_1 + w_{42} \times x_2 \end{bmatrix} \\ &= \begin{bmatrix} 0.1 \times 0.35 + 0.8 \times 0.9 \\ 0.4 \times 0.35 + 0.6 \times 0.9 \end{bmatrix} \\ &= \begin{bmatrix} 0.755 \\ 0.68 \end{bmatrix} \end{align*}$$

那么:

$$\begin{align*} y1 &= \begin{bmatrix} y_3 \\ y_4 \end{bmatrix} = f(W0 \times X) = f\left(\begin{bmatrix} w_{31} & w_{32} \\ w_{41} & w_{42} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\right) \\ &= f\left(\begin{bmatrix} w_{31} \times x_1 + w_{32} \times x_2 \\ w_{41} \times x_1 + w_{42} \times x_2 \end{bmatrix}\right) \\ &= f\left(\begin{bmatrix} 0.755 \\ 0.68 \end{bmatrix}\right) \\ &= \begin{bmatrix} 0.680 \\ 0.663 \end{bmatrix} \end{align*}$$

同理可以得到:

$$\begin{align*} z2 &= w1 \times y1 = \begin{bmatrix} w_{53} & w_{54} \end{bmatrix} \times \begin{bmatrix} y_3 \\ y_4 \end{bmatrix} \\ &= \begin{bmatrix} w_{53} \times y_3 + w_{54} \times y_4 \end{bmatrix} \\ &= \begin{bmatrix} 0.801 \end{bmatrix} \end{align*}$$

$$\begin{align*} y2 &= f(z2) = f(w1 \times y1) = f\left(\begin{bmatrix} w_{53} & w_{54} \end{bmatrix} \times \begin{bmatrix} y_3 \\ y_4 \end{bmatrix}\right) \\ &= f\left(\begin{bmatrix} w_{53} \times y_3 + w_{54} \times y_4 \end{bmatrix}\right) \\ &= f\left(\begin{bmatrix} 0.801 \end{bmatrix}\right) \\ &= \begin{bmatrix} 0.690 \end{bmatrix} \end{align*}$$

那么最终的损失为:

$C=\frac{1}{2}(0.690-0.5)^2 = 0.01805$

这也就是我们的目标函数, 我们的目标就是通过调整权重矩阵W0和W1, 让损失函数C最小! 这里用的方法就是梯度下降法, 接下来看看如何进行反向传播

$$\left\{ \begin{align*} C &= \frac{1}{2}(y_2 - y_{out}) \\ y_2 &= f(z_2) \\ z_2 &= (w_{53} \cdot y_3 + w_{54} \cdot y_4) \end{align*} \right.$$

那么我们可以通过链式法则, 求出损失函数C对$w_{53}$的偏导数:

$$\begin{align*} \frac{\partial C}{\partial w_{53}} &= \frac{\partial C}{\partial y_5} \cdot \frac{\partial y_5}{\partial z_5} \cdot \frac{\partial z_5}{\partial w_{53}} \\ &= (y_5 - y_{out}) \cdot f'(z_2) \cdot (1 - f(z_2)) \cdot y_3 \\ &= (0.69 - 0.5) \cdot (0.69) \cdot (1 - 0.69) \cdot 0.68 \\ &= 0.02763 \end{align*}$$

其中 sigmod 函数的导数为:

$$\begin{align*} f(x) &= \frac{1}{1 + e^{-x}} \\ f'(x) &= -(\frac{1}{1 + e^{-x}})^2 \cdot (-e^{-x})\\ &= \frac{1}{1 + e^{-x}} \cdot (1 - \frac{1}{1 + e^{-x}}) \\ &= f(x) \cdot (1 - f(x)) \end{align*}$$

同理可得:

$$\begin{align*} \frac{\partial C}{\partial w_{54}} &= \frac{\partial C}{\partial y_5} \cdot \frac{\partial y_5}{\partial z_5} \cdot \frac{\partial z_5}{\partial w_{53}} \\ &= (y_5 - y_{out}) \cdot f(z_5) \cdot (1 - f(z_5)) \cdot y_4 \\ &= (0.69 - 0.5) \cdot (0.69) \cdot (1 - 0.69) \cdot 0.663 \\ &= 0.02711 \end{align*}$$

现在我们继续求其他的偏导数

$W_{31},W_{32},W_{41},W_{42}$

给出其中一个的求导过程, 其他的类似

$$\left\{ \begin{aligned} C &= \frac{1}{2}(y_5 - y_{out})^2 \\ y_5 &= f(z_5) \\ z_5 &= (w_{53} * y_3 + w_{54} * y_4) \\ y_3 &= f(z_3) \\ z_3 &= w_{31} * x_1 + w_{32} * x_2 \end{aligned} \right.$$

$$\begin{align*} \frac{\partial C}{\partial w_{31}} &= \frac{\partial C}{\partial y_5} * \frac{\partial y_5}{\partial z_5} * \frac{\partial z_5}{\partial y_3} * \frac{\partial y_3}{\partial z_3} * \frac{\partial z_3}{\partial w_{31}} \\ &= (y_5 - y_{out}) * f(z_5) * (1 - f(z_5)) * w_{53} * f(z_3) * (1 - f(z_3)) * x_1 \end{align*}$$

最终的结果为:

$$\left\{ \begin{aligned} w_{31} &= w_{31} - \frac{\partial C}{\partial w_{31}} = 0.09661944 \\ w_{32} &= w_{32} - \frac{\partial C}{\partial w_{32}} = 0.78985831 \\ w_{41} &= w_{41} - \frac{\partial C}{\partial w_{41}} = 0.39661944 \\ w_{42} &= w_{42} - \frac{\partial C}{\partial w_{42}} = 0.58985831 \end{aligned} \right.$$